韦伯费希纳定律
代表了心理量出现偏差与物理量之间的关系。
ΔI(差别阈限)/I(标准刺激强度)=k(常数/韦伯分数)
dP = k * dS / S
该定律有很广泛的应用,比如更愿意在买一个50000元的电脑时花300块加个内存,而不愿意在5000块钱的电脑上加个300块的内存。
游戏中,随着某个数值自身的增加,需要更大的数值偏差才能刺激到玩家。
暗黑破坏神3就是一个简单粗暴的采用该定律的游戏。
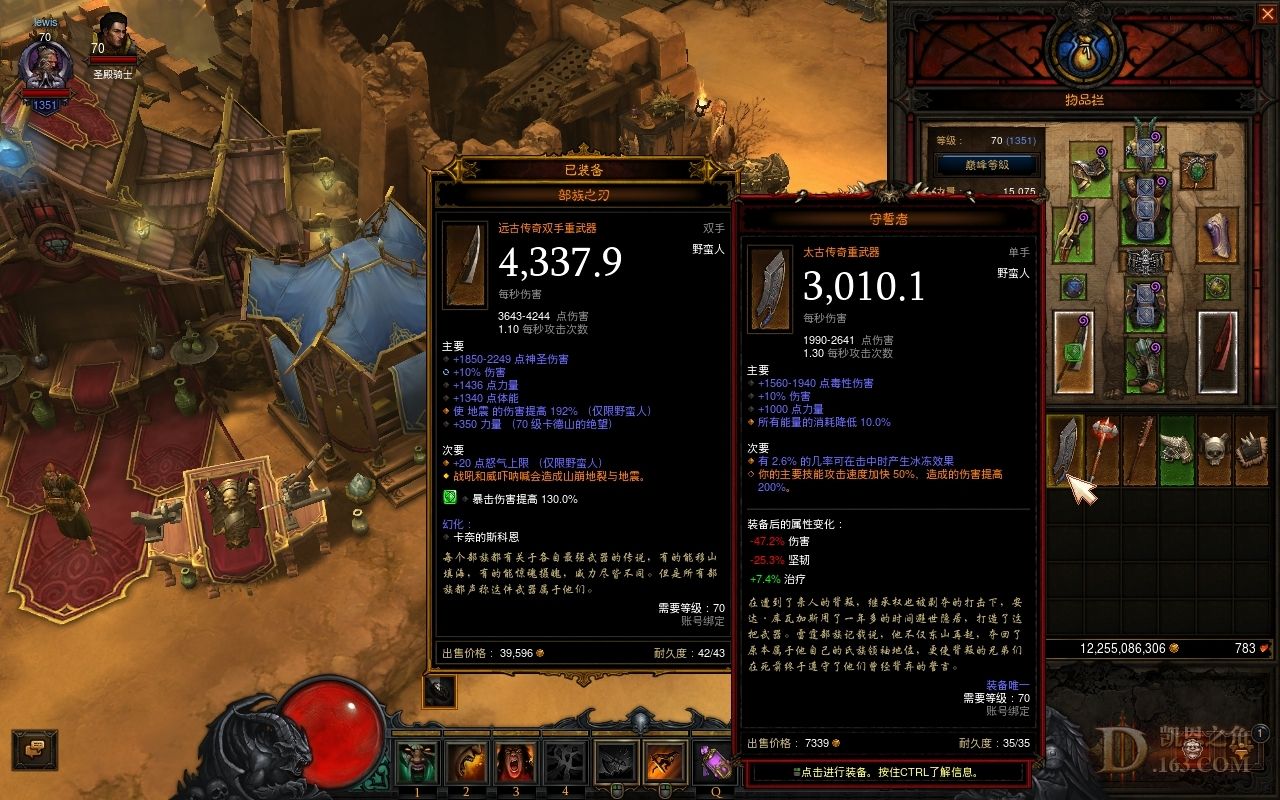

但是随着版本更迭动辄十亿,百亿的伤害让玩家对伤害数值等逐渐麻木,后续再添加新功能时就很难更改了做PVP内容也变得很不容易「暗黑3直接取消了PVP」
所以一般的游戏会采用以下两种方式去延长数值膨胀。
多层数值体系
采用多层数值来重置刺激。
血量、攻击、防御作为基础层的数值,在过多的使用之后会导致I越来越大,所需要的ΔI也越大,导致数值系统加速贬值。
在这种情况下会增加新的数值变量来重置刺激。这时候暴击、极速、命中、闪避等等就作为进阶层的数值来提供。
在提供进阶数值时要保证进阶数值的差异性与深入性,也就是要让玩家觉得更有价值「炫酷的暴击特效,独立的加成系数等」。
在进阶层的数值之上可能还会设计一些属性攻击等更深入的数值。
一般在卡牌养成手游中会更多的使用多层次的数值体系,一方面回归玩家的刺激值,另一方面能更好的与独立版本的养成点相结合。
社交刺激与目标性
随着数值层级的增多,带了点一个弊端就是新玩家的门槛不断在提高。所以在一些MMO中一般数值体系不会特别复杂,但是会有一些目标性和社交差异性的数值体现。
比较经典的就是魔兽世界中的蛋刀。
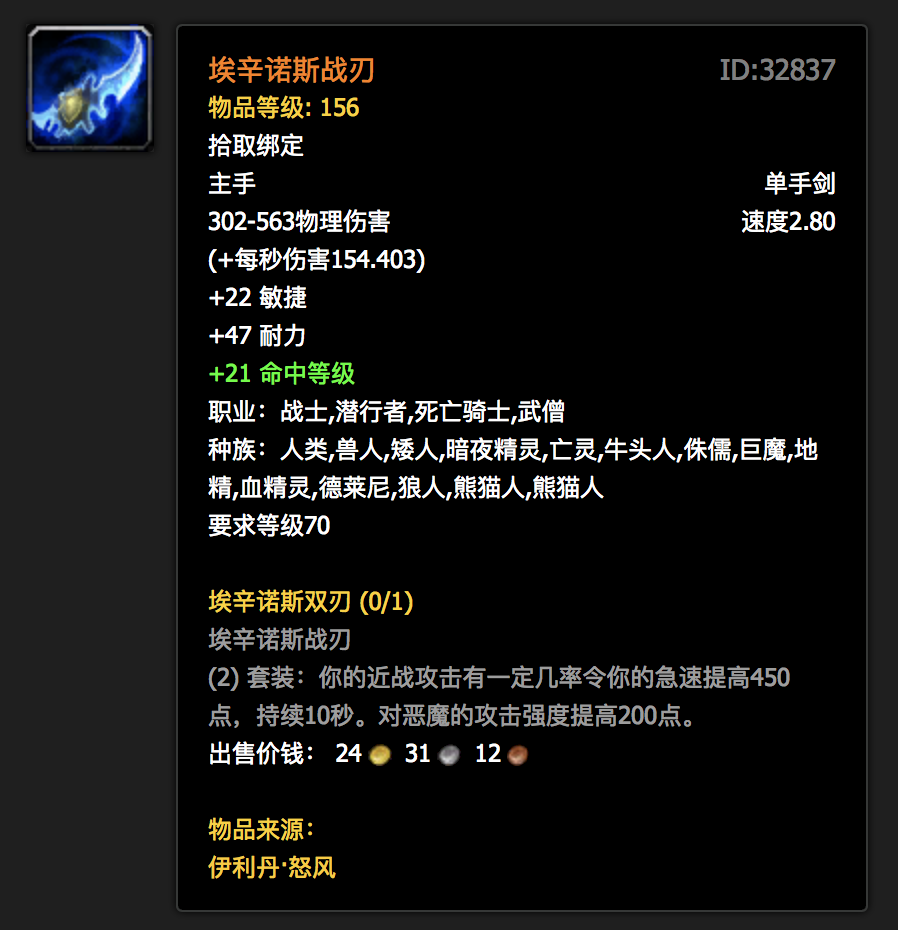

蛋刀属性固然很强,但是围绕他的社交属性:橙色的品质、独特的外形、光荣事迹等等。蛋刀不仅仅是数值的提升,也代表了公会的实力和人品。
所以蛋刀带来的成就感和满足感不是单一数值上的。一些社交类的游戏也通过一些版本Bis的装备来质变玩家的刺激。
欢迎各位讨论和指正。
本文内容原创,转载请注明出处。